UMass Amherst researchers weave two fundamental ideas of geometry and mechanics in a new theory of how thin sheets can be forced to conform to ‘geometrically incompatible’ shapes
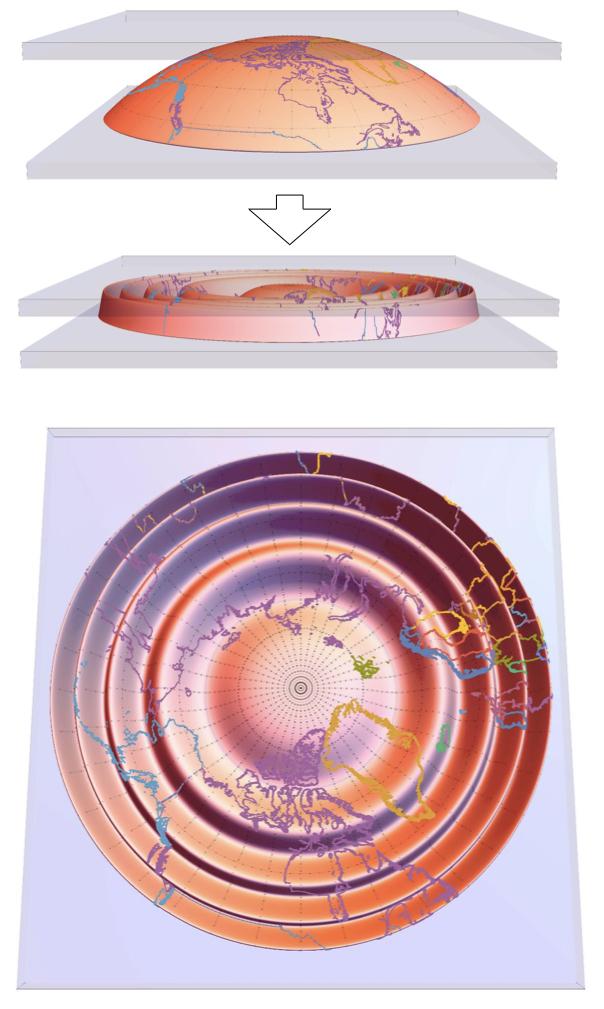
Credit: UMass Amherst/G. Grason
AMHERST, Mass. – Addressing a physics problem that dates back to Galileo, three University of Massachusetts Amherst researchers this week propose a new approach to the theory of how thin sheets can be forced to conform to “geometrically incompatible” shapes – think gift-wrapping a basketball – that relies on weaving together two fundamental ideas of geometry and mechanics that were long thought to be irreconcilable.
Theoretical physicist Benny Davidovitch, polymer scientist Greg Grason and doctoral student Yiwei Sun, writing in Proceedings of the National Academy of Sciences, suggest and demonstrate via numerical simulations that naturally flat sheets forced to change their curvature can accommodate geometrically-required strain by developing microscopic wrinkles that bend the sheet instead of stretching it to the breaking point, a solution that costs less energy, as well.
This advance is important as biotechnologists increasingly attempt to control the level of strain encountered in thin films conforming to complex, curving and 3D shapes of the human body, for example, in flexible and wearable sensors for personalized health monitoring, they explain. Many of these devices rely on electrical properties of the film which is shown to be highly vulnerable to stretching, but which can tolerate some bending.
The new concept is one of “close enough,” Davidovitch says – noncomformities that come with bending are so small that in practical terms, they cost almost no energy. “By offering efficient strategies to manage the strain, predict it and control it, we offer a new quantitative tool that’s useful for people predicting the forces required to emboss or wrap nanoscopic thin sheets and shells onto substrates of different shapes,” they state.
He adds, “Our work shows that by allowing tiny wrinkles in the wrapper, the necessary amount of stretching drops dramatically. For an extremely thin wrapper such as available today in laboratories, the stretching can be eliminated almost entirely.”
Grason points out, “Our theoretical framework provides a simple and adaptable tool for understanding how to control and manipulate, and ideally to optimize, the level of strain that a given geometry imposes on such a device, and thereby improve its performance.”
Davidovitch says there are two types of scientist interested in this long-standing problem, one less motivated by practicality than by how the laws of Nature apply. These thinkers are familiar with “Galileo’s beam,” a mechanics/physics problem that imagined a beam sticking out of a stone wall that will bend or deform when weight is added to it, he notes. Predicting the forces and strain on it posed a long-standing puzzle.
Galileo did not solve how much the beam will deform or how to predict that, he notes, but this problem related to strain was later explored and defined through new approaches to the geometry of continuous objects by German mathematician and physicist Carl Friedrich Gauss. Physicists and mathematicians “have focused a lot of intellectual activity over the centuries on it,” Davidovitch says.
After Galileo, Davidovitch say, Swiss mathematician Leonhard Euler developed the “elastica theory,” which argues that confined objects buckle in order to avoid strain, that is, any change in length. Euler showed that a situation in which absolutely no stretching takes place can occur under special circumstances, but not in the general type of confinement defined by Gauss’s geometrical constraints, he adds.
The UMass Amherst team’s new tool shows – when a constraint cannot be perfectly satisfied but almost satisfied – how to find the physical state or shape that’s the best fit. “It’s a new branch of variational calculus,” Davidovitch says. “All I need to do is minimize the curvature that nearly eliminates all stretching, and it lets me find the one with the smallest possible bending energy.”
They propose a new principle, the Gauss-Euler elastica, that reconciles the two cornerstones of classical mechanics and geometry defined previously by the works of Euler and Gauss. They invoke a new regime of solutions of the complex morphologies of thin bodies, a problem of intense recent interest from biophysics and materials engineering to applied mathematics, Grason points out.
He recalls, “When we first started this line of research, we didn’t imagine how it would turn out. We were not trying to solve this problem.” But doctoral student Sun, running some computer simulations, came up with results that defied naïve assumptions that confinement requires more energy to stretch than to bend the sheet. Formulas that he and Grason proposed were “impossible,” Davidovitch says, “they appeared to be violating fundamental geometrical theorems.”
They were stuck for two years, until they remembered Galileo’s beam, what Davidovitch calls a “thought contradiction,” that re-framed the question. It has been “very satisfying” to bring a new conceptual tool to the problem that wasn’t available before, he says. Grason adds, “It’s great to have an answer to why our initial simulations behaved so weirdly, of course. But eventually it leads us to understand the question better, and how it addresses a much broader class of problems in a new way. Yes, this has a good feeling.”
###
Media Contact
Janet Lathrop
[email protected]
413-545-2989
Original Source
https:/
Related Journal Article
http://dx.