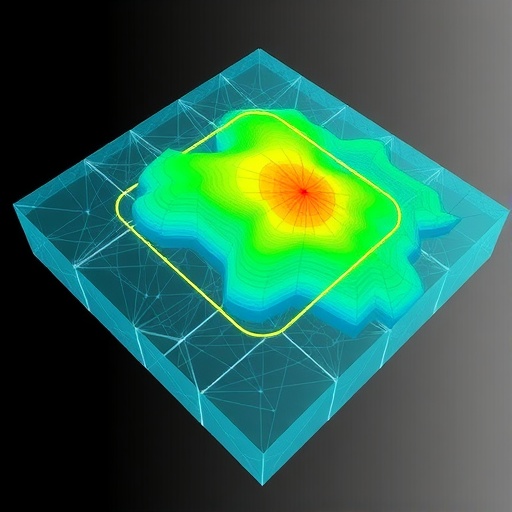
In the intricate world of physical networks, the three-dimensional arrangements we observe—whether in the brain’s neural wiring, vascular systems, or even natural structures like corals and trees—are influenced by complex developmental and functional imperatives. Until recently, it was widely believed that these vast networks evolved under competing pressures that would ultimately overshadow simple minimization principles. However, groundbreaking research reveals a surprising universality: the local architecture of these networks can be accurately predicted by a process of surface minimization, a notion that challenges traditional views on network optimization.
Physical networks are subject to a myriad of constraints. The brain’s neural networks, for instance, navigate complex biochemical cues during development, while vascular systems must balance efficient nutrient transport against the material costs involved in constructing and maintaining blood vessels. Intuitively, such systems should reflect a multitude of trade-offs, with holistic functional needs overriding purely geometric or cost-saving principles. Yet, the latest empirical studies demonstrate that a local surface minimization process robustly explains their branching morphology across diverse biological contexts, suggesting that cost efficiency remains a fundamental guiding factor at the microscale.
What is particularly striking about this discovery is the consistency with which it applies across vastly different physical systems. From neuronal trees to coral branches, the skeleton-like structures show morphological branching characteristics that align closely with solutions generated by minimizing surface area locally. This finding indicates that beyond broader evolutionary and functional demands, there exists a stereotypic structural principle rooted in minimizing surface energy, which appears to be leveraged repeatedly by nature during network formation.
Nevertheless, while this local optimization principle governs branch formation and junction design, it does not necessarily dictate global network properties. For example, the total lengths of these physical networks consistently exceed predictions based solely on Steiner’s minimal wiring theory by approximately 25%. This discrepancy points to the presence of additional constraints or functional requirements that compel networks to deviate from the theoretical optimum in pursuit of other critical objectives, such as robustness or signaling fidelity.
Further empirical work is essential to validate surface minimization models in more complex and large-scale networks that extend beyond locally tree-like architectures. Larger network constructs could reveal whether unique geometric adaptations occur as a function of specific systemic pressures. Features such as variable link thickness, curvature, or more intricate morphologies may be essential in meeting specialized demands like flow conservation in vascular networks or precise neuron placement in brain tissue, which remain beyond the current framework’s predictive capacity.
The current model predicts idealized structures consisting of uniform, straight cylindrical links far from branching points, lacking the capacity to address phenomena like loops—a hallmark of engineered systems such as traffic grids and power distribution networks. These loops represent a fundamental departure from simple wiring efficiency and require an expanded theoretical treatment that accounts for the complex interplay between redundancy, resilience, and cost. Developing such an extended framework could radically enhance our understanding of how diverse networks balance competing optimization criteria.
Intriguingly, the interplay between surface and volume considerations remains an open question. While blood vessels primarily reflect costs associated with surface area, neuronal and arboreal branches must factor the volumetric investment more heavily. Existing volume optimization models assume simplistic cylindrical links and often ignore the complex junction geometries inherent in real networks. The currently employed “min-surf-netw” algorithm, inspired by string-theoretic principles, focuses exclusively on surface minimization but hints at a close relationship between minimal surface configurations and near-optimal volumetric forms.
This synergy suggests that minimal surfaces might provide valuable approximations for volume-efficient morphologies as well, underscoring a deep geometric connection between surface and volumetric minimization strategies. Nevertheless, more sophisticated models that reconcile volume and surface considerations holistically could uncover fundamentally new network shapes and branching patterns that are inconceivable within the current theoretical landscape.
Beyond capturing the skeleton of these networks, a vital next step involves direct comparison of the predicted manifold geometries with detailed empirical measurements of local geometric features. These include surface geodesics, curvatures, and smoothness at branching points. Early results affirm that trifurcation junctions exhibit remarkable smoothness and symmetrical morphology in accordance with surface minimization predictions, providing compelling evidence that nature exploits these geometric constraints to achieve optimality at a fine scale.
This finding not only strengthens the empirical foundation of the surface minimization framework but also opens exciting prospects for more granular theoretical and experimental exploration. Understanding how small-scale local geometry emerges from optimization principles provides new insight into the fundamental design rules governing physical networks and how these might translate to functional advantages such as mechanical stability or efficient signaling.
Looking ahead, the integration of factors such as spatial crowding, physical knotting, and bundling of links into the surface minimization paradigm could dramatically expand the model’s explanatory power. These factors are pivotal in shaping real-world network organization and likely play crucial roles in reconciling efficiency with functional demands. Advances in computational methods and imaging technologies are poised to enable such sophisticated analyses, promising to elucidate the nuanced interplay between geometric constraints and biological or engineered functionality.
Ultimately, this research heralds a paradigm shift in our understanding of physical network design. Rather than viewing evolutionary and functional pressures as ultimately overriding geometric optimization, it appears that local surface minimization serves as a foundational principle upon which more complex and adaptive network functionalities are built. The hierarchical emergence of global network properties from local geometric minimality could represent a universal organizing principle in natural and artificial systems alike.
As efforts continue to broaden the scope and resolution of these investigations, we may gain profound insights into how different classes of physical networks manifest unique adaptations arising from distinct optimization landscapes. Such knowledge holds promise not only for fundamental biology but also for inspiring novel engineering solutions that mimic nature’s elegant efficiency in diverse applications ranging from neural prosthetics to vascular tissue engineering.
This multidisciplinary endeavor, blending geometry, physics, biology, and network science, exemplifies the power of theoretical modeling combined with empirical validation to uncover hidden organizing principles in complex living systems. The journey toward a comprehensive understanding of physical network design is ongoing and poised to reveal even more surprising connections at the interface of form, function, and efficiency.
Subject of Research: Physical networks and their geometric optimization principles in biological and natural systems.
Article Title: Surface optimization governs the local design of physical networks.
Article References: Meng, X., Piazza, B., Both, C. et al. Surface optimization governs the local design of physical networks. Nature 649, 315–322 (2026). https://doi.org/10.1038/s41586-025-09784-4
Image Credits: AI Generated
DOI: 10.1038/s41586-025-09784-4
Keywords: physical networks, surface minimization, branching morphology, optimization, vascular systems, neuronal networks, volume optimization, network geometry, bio-inspired design
Tags: branching morphology in natureconstraints in physical network developmentcost efficiency in biological structuresempirical studies on network morphologyfunctional imperatives in neural networkslocal architecture of neural wiringminimization principles in physical systemssurface optimization in biological networksthree-dimensional network arrangementstrade-offs in vascular system designuniversality of network optimizationvascular system design principles