Equivariant representations for molecular Hamiltonians and N-center atomic-scale properties

In the fields of chemistry and materials, most successful, widely used machine learning schemes introduced over the last decade aim to model molecular energies or interatomic potentials. Accordingly, the representations used to map atomic configurations into vectors of descriptors or features used as model inputs reflect fundamental properties of the interatomic potential such as invariance to permutation between identical atoms, rigid rotation or inversion of the molecular structure. They also reflect notions of locality and nearsightedness – the idea that potential, local electronic properties, depend significantly on the effective external potential only at nearby points – of many components of interatomic energy.

 This focus, particularly on locality and nearsightedness, has led to the use of atom-centered features that describe the arrangement of neighbors around a specific atom. Such atom-centered representations have been used to build models of properties such as NMR chemical shieldings, which are associated with an individual atomic center i, but also to express global properties such as the molecular energy as a sum of atom-centered contributions.

More recently, the need to construct data-driven models for atomic properties such as dipole moments and polarizabilities, which have more complicated structures, has led to the generalization of symmetry-invariant models. Though this results in equivariant behavior with respect to rotations and inversion, the representations are generally still used together with atom-centered frameworks. This is problematic because several properties, such as J-couplings in NMR, which describe the magnetic interaction between nuclear spins, or the matrix elements of a one-particle, effective electronic Hamiltonian Ĥ when written in an atomic orbital basis, are intrinsically associated with multiple atomic centers.  

Improved semiempirical methods could then be obtained through the construction of data-driven models that more closely match explicit electronic structure calculations. A machine-learned Ĥ could, for instance, allow researchers to access observables such as optical excitations, or could be used as an input in an emerging family of ML models that predict molecular properties using matrix elements computed by explicit electronic-structure calculations or corresponding eigenvalues. Existing ML approaches that attempt to predict the molecular Hamiltonian do so through ad-hoc modification of atom-centered features or by devising pair features: they don’t include rotational symmetries explicitly and instead rely on data augmentation to incorporate them into the model.  

Looking to provide a more solid mathematical basis to the problem of predicting these kinds of properties, researchers Michele Ceriotti, Jigyasa Nigam and Michael Willatt, all of the Laboratory of Computational Science and Modelling (COSMO) at EPFL, have introduced a symmetrized N-center representation that provides a natural, fully equivariant framework for learning properties associated with N atoms.  

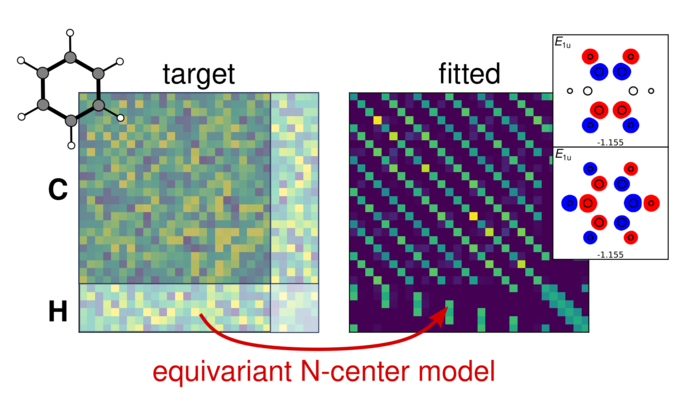
Combining atomic index and geometric equivariance requires separating the entries of the Hamiltonian matrix into blocks with well-defined symmetry behavior but leads to simpler models with fewer reference configurations that are sufficient to achieve robust, accurate predictions of Ĥ. Notably, the model accounts for both the general symmetries that are explicitly built in, but also those associated with specific point-group symmetries, when present. That is, the model is constructed to incorporate textbook molecular orbital theory. 

After demonstrating these fundamental properties on simple examples by examining the role of the orbital basis on model performance, the researchers went on to benchmark the method on problems of increasing complexity. They found that the approach gives excellent accuracy for a homogeneous dataset of distorted H₂O molecules, with linear regression achieving accuracy comparable to non-symmetry-adapted deep learning models, but with just a fraction of the training set size. Work on more complicated systems such as ethanol or a dataset of small organic molecules made it clear that focusing the ML exercise on the most relevant part of the electronic energy states—that is, disregarding the high-energy empty states—is at least as important as the details of the ML approach. One way of doing this, explored in their work, is to introduce a symmetry-adapted projected Hamiltonian, a smaller matrix that only reproduces valence and low-lying, unoccupied eigenstates while retaining all other geometric symmetries. 

The researchers conclude that symmetry-adapted, atom-permutation and rotation equivariant representations are competitive with state-of-the-art, deep-learning models despite the use of only linear or kernel regression and are suitable for describing quantities associated with multiple atomic centers. The N-center representations could also be readily applied to the condensed phase. The next step, in terms of building fully equivariant descriptors of N-center atomic clusters, will be to introduce higher-body-order terms either explicitly or through more sophisticated nonlinear models.  

“The general construction we present here provides an easily-extendable framework to do so, as well as to tackle the modeling of 3-center integrals, and higher-N quantities, bringing the full set of ingredients of quantum chemistry calculations within the reach of equivariant machine learning schemes,” the researchers said.