Are birds flying atoms?

A crowd or a flock of birds have different characteristics from those of atoms in a material, but when it comes to collective movement, the differences matter less than we might think. We can try to predict the behavior of humans, birds, or cells based on the same principles we use for particles. This is the finding of a new study published in the Journal of Statistical Mechanics: Theory and Experiment, JSTAT, conducted by an international team that includes the collaboration of MIT in Boston and CNRS in France. The study, based on the physics of materials, simulated the conditions that cause a sudden shift from a disordered state to a coordinated one in “self-propelled agents” (like biological ones).

“In a way, birds are flying atoms,” explains Julien Tailleur, from MIT Biophysics, one of the authors of the research. “It may sound strange, but indeed, one of our main findings was that the way a walking crowd moves, or a flock of birds in flight, shares many similarities with the physical systems of particles.”

As Tailleur explains, in the field of collective movement studies, it has been assumed that there is a qualitative difference between particles (atoms and molecules) and biological elements (cells, but also entire organisms in groups). It was especially believed that the transition from one type of movement to another (for example, from chaos to an orderly flow, known as a phase transition) was completely different.

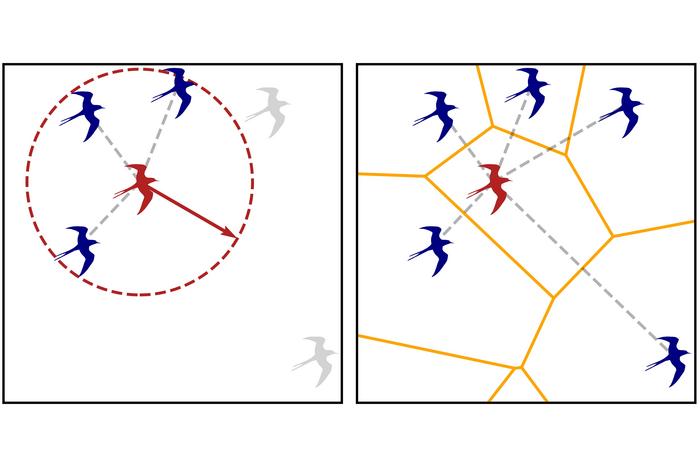
The crucial difference for physicists in this case has to do with the concept of distance. Particles moving in a space with many other particles influence each other primarily based on their mutual distance. For biological elements, however, the absolute distance is less important. “Take a pigeon flying in a flock: what matters to it are not so much all the closest pigeons, but those it can see.” In fact, according to the literature, among those it can see, it can only keep track of a finite number, due to its cognitive limits. The pigeon, in the physicists’ jargon, is in a “topological relationship” with other pigeons: two birds could be at quite a large physical distance, but if they are in the same visible space, they are in mutual contact and influence each other.

It was long believed that this type of difference led to a completely different scenario for the emergence of collective motion  “Our study, however, suggests that this is not a crucial difference,” continues Tailleur.

“Obviously, if we wanted to analyze the behavior of a real bird, there are tons of other complexities that are not included in our model. Our field follows an advice attributed to Einstein, namely that if you want to understand a phenomenon, you have to make it ‘as simple as possible, but not simpler’. Not the simplest possible, but the one that removes all complexity that is not relevant to the problem. In the specific case of our study, this means that the difference that is real and exists – between physical distance and topological relationship – does not alter the nature of the transition to collective motion.”

The model used by Tailleur and colleagues is inspired by the behavior of ferromagnetic materials. These materials have – as the name suggests – magnetic properties. At high temperature or low density, the spins (simplifying: the direction of the magnetic moment associated with electrons) are oriented randomly due to the large thermal fluctuations and are therefore disorderly. However, at low temperatures and high density, the interactions between the spins dominate the fluctuations and a global orientation of the spins emerges (imagining them as many aligned small compass needles).

“My colleague Hugues Chaté realized twenty years ago that, if the spins were to move in the direction in which they point, they would order through a discontinuous phase transition, with the sudden apparition of large groups of spins moving together, much like flocks of birds in the sky”, says Tailleur. This is very different from what happens in a passive ferromagnet, where the emergence of order occurs gradually. Until recently, physicists believed that biology-inspired models in which particles align with their `topological neighbors’ would also experience a continuous transition. In the model used in the study, Tailleur and colleagues showed that, instead, a discontinuous transition is observed, even if the topological relationship instead of distance is used, and that this scenario should apply to all such models. “Within some limits, the details of how you align is irrelevant”, says Tailleur, “and our work shows that this type of transition should be generic.” 

Another finding is that in the model used, stratified flows form within the larger group, which is akin to what we also observe in reality: it is rare for a mass of people to move all together in one direction; rather, we see within it the motion of finite groups, distinguishable flows that follow slightly different trajectories.

These statistical models, based on the physics of particles, can therefore also help us understand biological collective movement, concludes Tailleur. “The road towards understanding collective motion as we see it in biology—and using it to design new materials—is still long, but we are making progress!”