In the intricate world of particle physics, understanding the internal structure of hadrons—the building blocks of visible matter such as protons and neutrons—remains a formidable challenge. These composite particles are formed by quarks and gluons, collectively termed partons. The fundamental question is: how exactly do these partons distribute themselves within hadrons when the hadrons are moving at near-light speeds? This information is encoded in mathematical formulations known as parton distribution functions (PDFs). PDFs describe the probability of finding a parton carrying a certain fraction, denoted by x, of the hadron’s total momentum. Historically, physicists have relied heavily on experimental data amassed over decades and phenomenological modeling to extract PDFs, yet these approaches are fundamentally empirical and lack first-principles derivations grounded in Quantum Chromodynamics (QCD), the theory governing strong interactions.
.adsslot_6kOlZIF5GY{ width:728px !important; height:90px !important; }
@media (max-width:1199px) { .adsslot_6kOlZIF5GY{ width:468px !important; height:60px !important; } }
@media (max-width:767px) { .adsslot_6kOlZIF5GY{ width:320px !important; height:50px !important; } }
ADVERTISEMENT
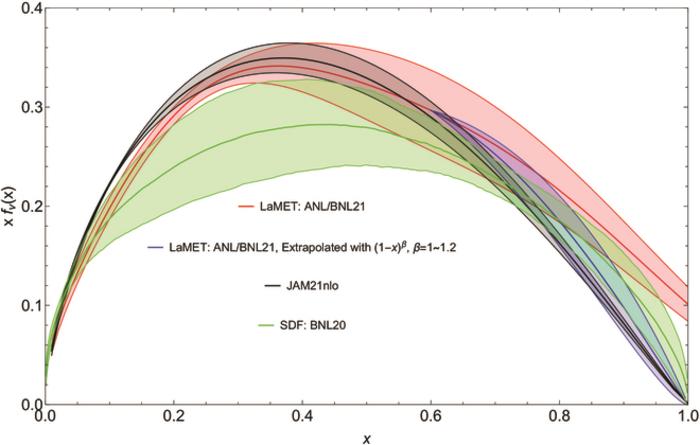
Another groundbreaking approach that has emerged is Large-Momentum Effective Theory (LaMET), which Xiangdong Ji of the University of Maryland first pioneered. LaMET enables lattice QCD calculations at large but finite hadron momenta, bridging the gap between Euclidean lattice computations and Minkowski light-cone physics. The key innovation lies in using boosted hadron states on the lattice, allowing quasi-distributions—lattice calculable objects in Euclidean space—to be matched perturbatively to true PDFs defined in light-cone coordinates. In the infinite momentum limit, LaMET quasi-PDFs converge to standard PDFs, while at finite momenta, sophisticated matching procedures correct approximations to produce explicit x-dependent distributions.
In a landmark study published in the journal Research on May 28, 2025, Distinguished University Professor Xiangdong Ji presented a thorough analysis comparing LaMET and SDE methodologies. His work highlights their complementary strengths and how a synergy between these approaches can significantly enhance the precision and reliability of lattice QCD-derived PDFs. “Both LaMET and SDE are widely studied approaches for calculating PDFs and have their strengths in different aspects,” Ji explains. By integrating global constraints from SDE and x-dependent precision from LaMET, researchers can develop a more holistic and accurate picture of parton dynamics within hadrons.
One of the major advantages of LaMET is its direct access to the x-dependence of PDFs over a wide intermediate momentum fraction range, typically spanning roughly from 0.1 to 0.7. This intermediate region is particularly relevant for many high-energy processes studied at particle colliders. However, at very small x (corresponding to partons carrying tiny fractions of momentum) and very large x (carrying near-total momentum), LaMET becomes less effective because the requisite hadron boost becomes unrealistically large, posing severe computational difficulties. Here, the SDE method complements by providing global moment constraints that effectively guide and stabilize the extrapolation of LaMET-calculated PDFs in these difficult-to-reach regions.
In practical terms, Professor Ji applied this combined framework to calculate the valence quark PDFs of pions, a system of fundamental interest given their role in the strong interaction and as probes in various experiments. The calculations utilized high-precision lattice QCD computations under the LaMET formalism, supplemented by phenomenological modeling aided with SDE global constraints. Crucially, these theoretical predictions matched remarkably well with experimental data from collaborations at Argonne and Brookhaven National Laboratories, validating the hybrid approach’s effectiveness.
The success of this research paves the way for generating state-of-the-art lattice QCD PDFs that can be used to make powerful predictions for high-energy particle collisions, such as those at the Large Hadron Collider. Enhanced precision in PDFs reduces uncertainties in theoretical models and may help reveal subtle signatures of new physics or novel hadronic phenomena previously obscured by theoretical limitations. This marks a critical stride toward first-principle, nonperturbative understanding of hadron structure—a longstanding quest in nuclear and particle physics.
Beyond immediate practical impacts, Ji’s study underscores a broader scientific narrative: the importance of methodological innovation and cross-validation in theoretical physics. The convergence of LaMET and SDE exemplifies how diverse frameworks can complement and reinforce each other, overcoming intrinsic limitations and deepening the insights into one of nature’s most fundamental forces, the strong interaction.
The implications also extend to other subfields. PDFs are indispensable in interpreting experimental results not only for protons and pions but also for more exotic hadrons and nuclei, thereby influencing research areas spanning from astrophysics to cosmology, where strong interaction physics plays a role in stellar evolution and the early universe.
Moreover, the refinement of lattice QCD techniques empowered by large-scale computational resources, combined with the new theoretical frameworks, heralds a new era where ab initio calculations of hadronic properties move from aspiration to reality. This progress will steadily reduce reliance on phenomenological fits, enabling truly predictive theoretical physics grounded in the fundamental axioms of QCD.
Professor Ji’s work exemplifies the power of theoretical ingenuity coupled with computational advancements, driving particle physics forward. His pioneering contributions to LaMET and his synthesis of complementary techniques represent a milestone in decoding the quark-gluon world—an achievement that will resonate throughout the physics community for years to come.
Subject of Research:
Ab initio calculations in lattice Quantum Chromodynamics focused on parton distribution functions within hadrons.
Article Title:
Ab Initio Lattice Quantum Chromodynamics Calculations of Parton Physics in the Proton: Large-Momentum Effective Theory versus Short-Distance Expansion
News Publication Date:
28-May-2025
Web References:
DOI: 10.34133/research.0695
Image Credits:
Professor Xiangdong Ji, University of Maryland, College Park, USA
Keywords
Lattice QCD, Parton Distribution Functions, Large-Momentum Effective Theory, Short-Distance Expansion, Quantum Chromodynamics, Hadron Structure, Pion Valence PDFs, Ab Initio Calculations, High-Energy Physics, Theoretical Particle Physics
Tags: computational challenges in QCDempirical vs first-principles approachesfirst-principles calculations in particle physicshadron momentum distributioninternal structure of hadronslattice QCD techniquesnonperturbative QCD methodsparticle physics research advancementsparton distribution functionsQuantum Chromodynamics applicationsquarks and gluons interactionsstrong force dynamics